There are various ways to calculate your return on investment. Industrial robots usually concentrate on the improvements in the rate or speed of the enhancement and calculate the quantity of product they can manufacture during a particular time frame. With a collaborative robot, the way of thinking can be quite different.First, cobots are not a lot faster than humans are and cannot carry a lot more weight. But, they can do the tasks that are redundant, dangerous or boring for a human worker. They can also be placed beside the worker to help him/her in their work. So, the ROI is not calculated on the increase in the production rate, but how you can produce more with the same quantity of resource. What I am trying to say is that most applications that are done by collaborative robots are done to free up the human worker for more dexterous or cerebral tasks.
The general way to calculate the ROI for collaborative robots is:
ROI = Investment [$] / Savings [$] = Time before it is complete repaid [years]
Where investment is defined as: the total of all expenses due to the robotic cell:
Investment [$]: Robot cost + gripper cost + design cost + installation time + shut down time + …
And savings is defined as: need explanation here
Savings [$] = Yearly Cost [$] – Potential Scenario [$] + Production Enhancement [$]
First, cobots are not a lot faster than humans are and cannot carry a lot more weight. But, they can do the tasks that are redundant, dangerous or boring for a human worker. They can also be placed beside the worker to help him/her in their work. So, the ROI is not calculated on the increase in the production rate, but how you can produce more with the same amount of resources. What I am trying to say is that most applications that are done by collaborative robots are done to free up the human worker for more dexterous or cerebral tasks
The general way to calculate the ROI for collaborative robots is:
ROI = Investment [$] / Savings [$] = Time before it is complete repaid [years]
Where investment is defined as: the total of all expenses due to the robotic cell:
Investment [$]: Robot cost + gripper cost + design cost + installation time + shut down time + …
And savings is defined as:
Savings [$] = Yearly Cost [$] – Potential Scenario [$] + Production Enhancement [$]
The yearly cost includes the cost to run a machine without a robot. So basically the number of employees on how many shifts and their respective salaries, plus the down time cost and the scrap cost for this particular process. Plus, the cost of the jig, etc. to execute the job.
The potential scenario is using the exact same variables, but incorporates cobots and this usually makes the process more cost effective. See the example below to get a better idea.
|
Savings:
|
|
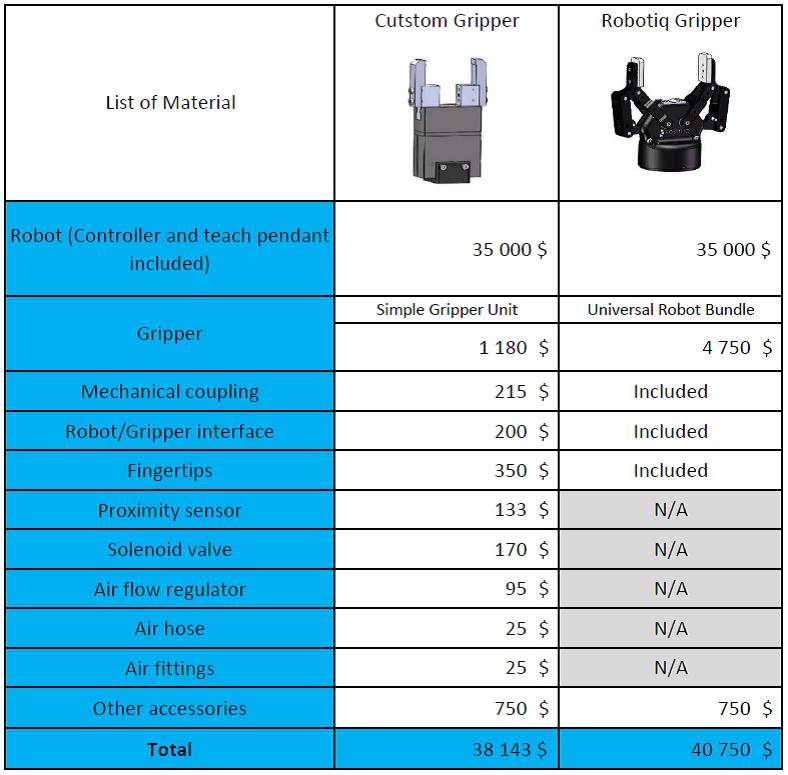
Investments: All the parts and accessories required to make your robotic cell work are listed in Table 3. This includes: the robot, the gripper and all the accessories required to install the robot correctly in the plant. Material Investment Custom Gripper = $38,143
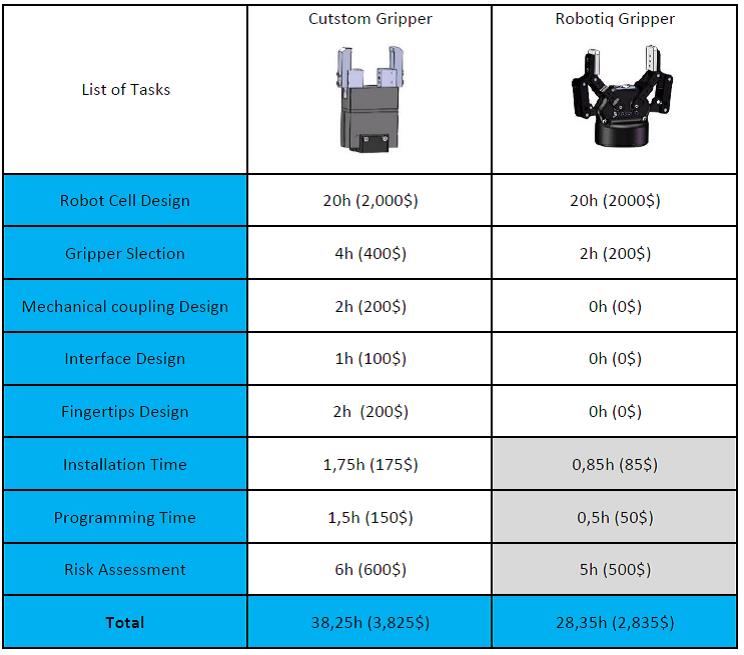
The investment also includes the time spent to design, select and install the robot and the Gripper on the shop floor.
|
So to evaluate the return investment we simply have to use the equation defined above:
ROI = Investments [$] / Savings [$]
In the case of the custom Gripper the return on investment would be:
ROI custom = $41,968/$62,000 = 0.68 years
Which represent a return on investment in 8.16 months.
In the other case, the return on investment of a Robotiq Gripper would be:
ROI Robotiq = $43,785 / $ 62,000 = 0.706 years
Which represents a return on investment of 8.4 months. So basically you get back your investment only 7 days after a custom gripper.
So what should I conclude?
Well, these are basically the same return on investments for a custom or flexible gripper. Even if the Robotiq Gripper is a little more expensive it might be worth the try. Because there are other arguments in favor of a flexible electric gripper. In fact, at the very moment you want to add other custom fingers or change your application, you will need to design, manufacture and install new fingers on your custom gripper which will increase your investment and will change the ROI. In the case of the Robotiq Adaptive Gripper, it can be repurposed pretty easily and be setup to work on a totally different application without any physical modifications. This means you can use your Gripper for more operations and it will have a:
- Comparable starting investment.
- Seamless and faster integration with the Robotiq Adaptive Gripper technology.
- Greater flexibility and possibility to repurpose the robot with a Robotiq Gripper.
Make sure to do your own ROI calculations for your robotic cell. The following documents should help you structure your analysis and help you consider more details about your process. Also it should give you more visual references to understand the ROI process.
Related Articles
WHICH ROBOT GRIPPER IS EASIER TO INTEGRATE? PART 1 - SELECTION PROCESS
WHICH ROBOT GRIPPER IS EASIER TO INTEGRATE? PART 2 - DESIGN PROCESS
WHICH ROBOT GRIPPER IS EASIER TO INTEGRATE? PART 3 - INTEGRATION PROCESS
Leave a comment